Remember that time in Geometry class when you stared at a circle, its lines, and angles, feeling completely lost? You weren’t alone. The world of secants, tangents, and angle measures can seem daunting at first. But just like navigating a maze, with practice and a clear understanding of the rules, you can master it! This article will equip you with the skills and confidence to tackle any problem involving these geometric concepts.

Image: www.teacherspayteachers.com
Think of your journey through the 9-6 Skills Practice as a grand adventure, much like a seasoned explorer setting out to discover uncharted territories. We’ll navigate the complexities of secants, tangents, and angle measures, equip you with the tools to conquer challenging problems, and leave you with a newfound appreciation for the beauty and logic of geometry. Let’s begin our exploration, one step at a time.
Demystifying the Basics: Understanding Secants, Tangents, and Their Relationship with Angles
Before embarking on our adventure, let’s ensure we have a solid foundation. It’s like gathering provisions before venturing into the unknown. So, let’s define our key terms.
Secants, Tangents, and Circles: Essential Definitions
Imagine a circle as a magical ring. A **secant** is like a thread that passes through the ring from one point on the circle to another, piercing right through the center. Think of it as a chord that goes beyond the circle’s boundary. On the other hand, a **tangent** is a thread that gently brushes against the ring at just one point. It’s like a line that skims the edge without going inside. These lines, along with the circle itself, create a myriad of angles, waiting to be explored.
Angles in the Circle: Unveiling the Secrets
The interplay between secants, tangents, and the circle creates a fascinating landscape of angles. An **inscribed angle** is formed by two secants (or tangents) that meet on the circle’s edge, while a **central angle** has its vertex (the point where the lines meet) at the center of the circle. We’ll delve deeper into how these angles are connected and how to calculate their measures.
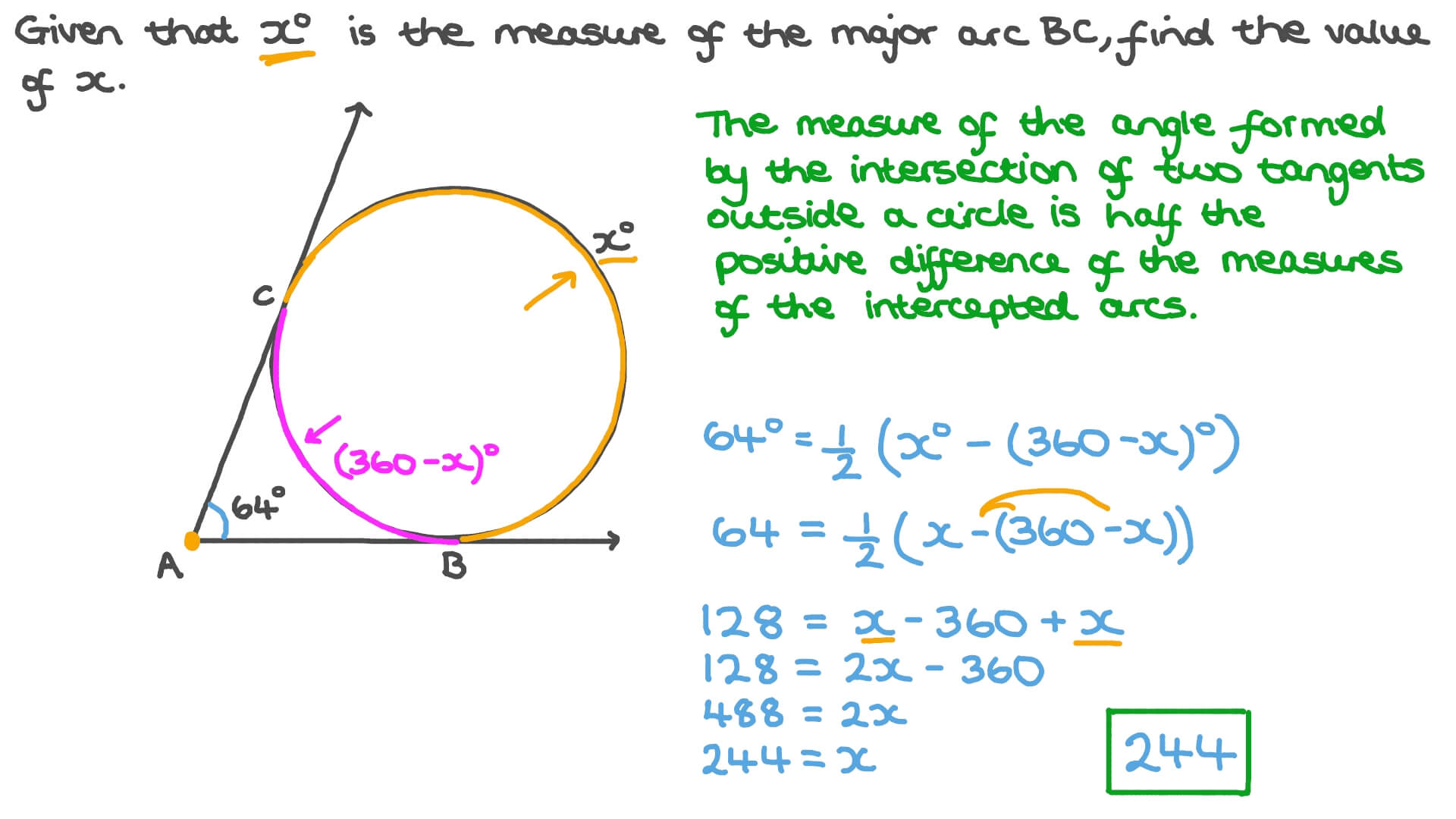
Image: www.nagwa.com
Essential Relationships: Building a Foundation
The relationship between these lines and angles is governed by some fundamental theorems. Inscribed angle theorem states that an inscribed angle’s measure is half the measure of the intercepted arc (the part of the circle’s circumference between the endpoints of the secants or tangents). Central angle theorem states that a central angle’s measure is equal to the measure of the intercepted arc. These theorems are our compass and map, guiding us through the intricacies of angle calculations.
Navigating the 9-6 Skills Practice: Strategies for Success
With our definitions and theorems in place, it’s time to conquer the 9-6 Skills Practice. Think of it as a series of challenges that test your understanding of the concepts we’ve explored. Mastering these skills will unlock the ability to solve any problem involving secants, tangents, and angles.
Visualizing the Problem: A Key To Success
Every problem in the 9-6 Skills Practice is a story waiting to be decoded. Start by visualizing the situation. Draw a diagram, carefully labeling the lines, angles, and points. This act of visual representation will bring clarity to the problem and reveal hidden relationships. Just like an explorer sketching a map on the terrain, diagramming helps you see the bigger picture.
Strategic Breakdown: Deconstructing Complex Problems
Once you have your diagram, break down the problem into smaller, manageable steps. Identify the known information, like the lengths of lines or the measures of certain angles. Then, use the theorems and relationships we’ve discussed to determine the unknowns. Think of it as a detective piecing together clues from a crime scene, each step leading you closer to a solution.
Practice Makes Perfect: Mastering the Art of Solving
The key to success is consistent practice. As you work through the 9-6 Skills Practice, treat each problem as an opportunity for learning. Don’t just aim for the right answer; focus on understanding the process, the reasoning behind each step. Work through different styles of problems, trying to recognize patterns and variations. The more you practice, the more your geometric intuition will develop. Just as a musician practices scales, consistent practice in geometry will make you a virtuoso of angles and lines.
Experts’ Advice: Strategies from the Professionals
As a seasoned traveler in the world of Geometry, I’ve gathered insights from experienced mathematicians and educators. Here are some tips that can elevate your understanding and problem-solving skills:
Embrace Failure: Learn From Mistakes
Don’t be discouraged by mistakes. They are simply stepping stones on your path to mastery. Every wrong answer is an opportunity to identify gaps in your understanding and refine your approach. Instead of viewing errors as setbacks, see them as valuable learning experiences.
Seek Help When Needed: Collaborate with Peers
Don’t hesitate to seek help when facing a difficult problem. Talk to your classmates, teachers, or online resources. Collaborative learning is a powerful tool for understanding complex concepts. Just like a team of explorers tackling obstacles together, sharing ideas and perspectives can unlock new insights.
Frequently Asked Questions: Addressing Common Concerns
During my journey through geometry, I encountered numerous questions that echoed across the classroom. Here are some of the most common ones, along with helpful answers to guide you.
Q: What are some common mistakes students make when working with secants and tangents?
A: A common mistake is misidentifying the relevant lines and angles. Carefully read the problem statement and ensure you correctly differentiate between secants, tangents, central angles, and inscribed angles.
Q: How can I tell if an angle is inscribed or central?
A: An inscribed angle’s vertex lies on the circle’s circumference, while a central angle’s vertex is at the circle’s center. Visualize the location of the angle’s vertex to determine its type.
Q: What are some real-life applications of these concepts?
A: Secants and tangents find applications in various fields, including architecture, engineering, and astronomy. For example, they are used in designing bridges, calculating distances between celestial bodies, and analyzing the paths of projectiles.
9-6 Skills Practice Secants Tangents And Angle Measures
Conclusion: Embark on Your Geometric Adventure
With a firm understanding of secants, tangents, and angle measures, you’ve conquered the fundamentals of the 9-6 Skills Practice. You now possess the tools and strategies to navigate any geometric problem that comes your way. Remember, the journey of mastering Geometry is an ongoing one! Keep practicing, exploring, and embracing challenges with curiosity and confidence.
Are you ready to embark on your own geometric adventure? Tell us about your experiences and insights in the comments below! Let’s continue learning and sharing our love of geometry together.




