Have you ever looked at a bridge and wondered how its intricate structure remains stable? Or admired the precise angles of a skyscraper, understanding that even the slightest deviation could lead to disaster? The principles behind these marvels are rooted in geometry, and understanding the relationship between parallel lines and proportional parts is key to unlocking these secrets. This study guide and intervention will unravel the fascinating world of parallel lines and proportional parts, opening doors to understanding not only the beauty of geometry but also its practical applications in everyday life.

Image: www.coursehero.com
Imagine you’re a carpenter working on a complex project involving multiple pieces of wood. How do you ensure the pieces fit together perfectly? How do you divide a given line segment into equal parts or proportionally to create a stunning design? The answer lies in the powerful concepts of parallel lines and proportional parts. These concepts aren’t just theoretical ideas; they are the backbone of numerous fields, including architecture, engineering, design, and even art.
Parallel Lines: The Foundation of Geometry
Parallel lines are like two straight roads that never meet, no matter how far they extend. They are a fundamental concept in geometry, and their importance lies in their predictable behavior. Think of a train track; the tracks are parallel, guaranteeing a smooth and consistent journey for the train. In geometry, we use the symbol “||” to denote parallelism. So, two lines, line “a” and line “b,” are parallel if we write them as “a || b.”
Types of Parallel Lines
Parallel lines are not always perfectly aligned, as they can have different orientations. This leads to the concept of transversal lines, which are lines that cut across a set of parallel lines. When a transversal line intersects parallel lines, it creates a variety of angles, each with unique properties:
-
Corresponding Angles: These angles are located in the same position relative to the parallel lines. They are congruent, meaning they have the same measure. Think of two windows on a building – the windows on the same side of the building and at the same level would be corresponding angles.
-
Alternate Interior Angles: These angles are located between the parallel lines, on opposite sides of the transversal. They are also congruent. Imagine a pair of scissors; the blades are parallel, and the opening between them represents the alternate interior angles.
-
Alternate Exterior Angles: These angles are located outside the parallel lines, on opposite sides of the transversal. They are congruent. Think of two parallel train tracks; observe the space between the tracks on opposite sides of the train.
-
Same Side Interior Angles: These angles are located between the parallel lines, on the same side of the transversal. They are supplementary, which means their sum is 180 degrees. Imagine two walls meeting at a corner; the angles formed by the walls and the floor represent same-side interior angles.
Understanding the relationships between these angles is crucial for solving problems involving parallel lines.
Proportional Parts and the Beauty of Division
Proportional parts go hand in hand with parallel lines, forming a harmonious relationship that enables precise division. This relationship manifests in various geometric figures, including triangles and other polygons.
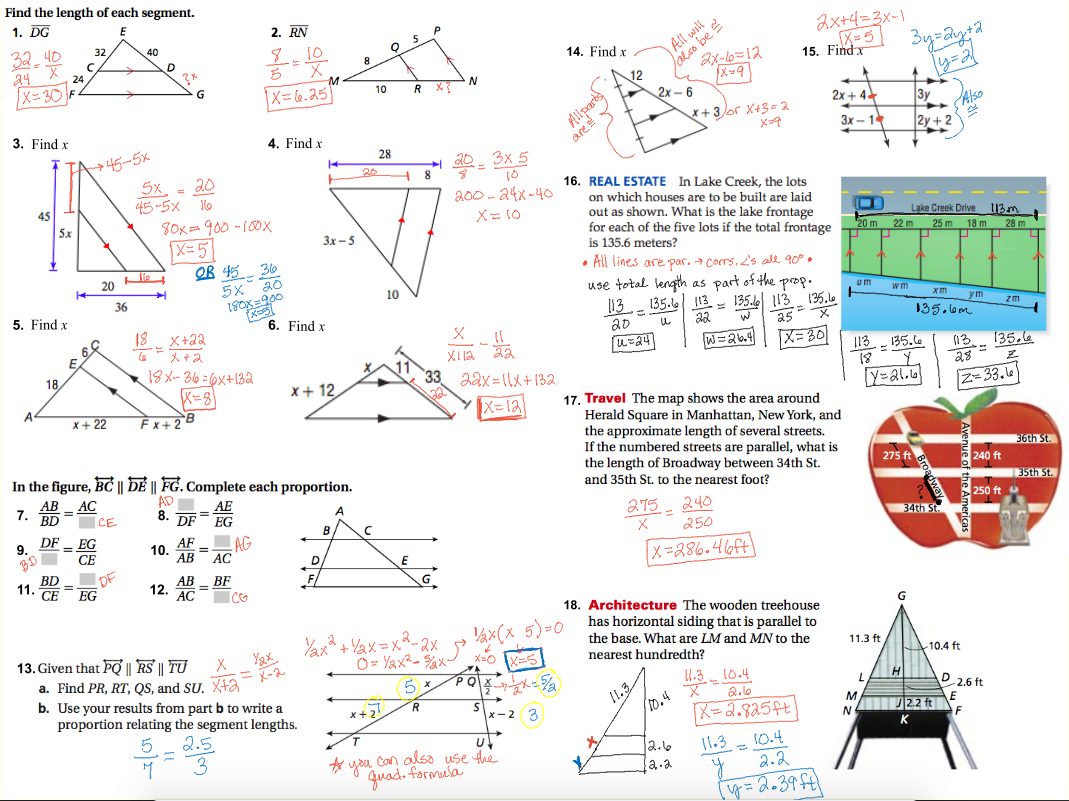
Image: amandapaffrath.weebly.com
Triangles and Proportional Parts
The foundational theorem governing proportional parts in triangles is the Parallel Proportionality Theorem. This theorem states that if a line is parallel to one side of a triangle and intersects the other two sides, then it divides those sides proportionally. Imagine drawing a line across a triangle, parallel to one side. This line creates smaller triangles within the larger triangle, and the ratio of the corresponding sides of these triangles is equal.
Consequences of the Parallel Proportionality Theorem
The Parallel Proportionality Theorem has far-reaching consequences, leading to several important corollaries, including:
-
Triangle Proportionality Theorem: This theorem states that if a line divides two sides of a triangle proportionally, then it is parallel to the third side. This is the converse of the Parallel Proportionality Theorem, establishing a reciprocal relationship between parallelism and proportionality.
-
Mid-segment Theorem: This theorem states that the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and half its length. This is a special case of the Parallel Proportionality Theorem, where the line dividing the sides is the mid-segment, which is a line segment connecting the midpoints of two sides of a triangle.
Application in Real-World Contexts
The concepts of parallel lines and proportional parts are not merely theoretical explorations; they have vital applications in real-world scenarios. Here are some examples:
-
Architecture: Architects use parallel lines and proportional parts to design structures that are visually appealing, structurally sound, and functional. The parallel lines in a building’s facade provide stability, while proportional parts ensure that windows, doors, and other features are scaled appropriately.
-
Construction: Civil engineers rely heavily on parallel lines and proportional parts to ensure that roads, bridges, and buildings are built with precision, optimizing functionality and safety.
-
Design: Designers in various fields, from graphic design to fashion, use these concepts to create aesthetically pleasing and balanced compositions.
-
Art: Artists utilize parallel lines and proportional parts to create perspective, depth, and realism in their works.
Expert Insights and Actionable Tips
To master the concepts of parallel lines and proportional parts, here are some invaluable insights from renowned mathematicians and educators:
-
Visualize the concepts: Draw diagrams and use visual aids to grasp the relationships between parallel lines, transversal lines, and proportional parts. Imagine how these concepts are applied in real-world scenarios.
-
Practice problem-solving: Solve a wide range of problems involving parallel lines, proportional parts, and the theorems discussed above. Start with basic problems and gradually move towards more complex ones.
-
Seek help when needed: Don’t be afraid to ask your teacher or a tutor for clarification on any aspect you find challenging. There are numerous online resources and learning platforms that can provide additional support.
7-4 Study Guide And Intervention Parallel Lines And Proportional Parts
Conclusion
As we’ve explored the fascinating world of parallel lines and proportional parts, we’ve uncovered their intricate relationships, their profound impact on geometry, and their breadth of real-world applications. From the stability of bridges to the beauty of art, these concepts are fundamental to our understanding of the world around us. By mastering these concepts, you unlock a key to understanding the universe’s hidden geometry, allowing you to see things in a new light. So, whether you are an aspiring architect, artist, or simply a curious mind, embrace these concepts, and let them illuminate your path to a deeper understanding of the world around you.




