Remember that frustrating moment in geometry class when you just couldn’t grasp the concept of parallel and perpendicular lines? The seemingly endless theorems and confusing diagrams had me feeling overwhelmed. Luckily, my teacher introduced us to a simple trick that changed everything – breaking down complex concepts into smaller, manageable steps. Whether you’re struggling with a specific problem or just want to solidify your understanding of parallel and perpendicular lines, this guide will help you unlock the secrets of Unit 3.

Image: www.pdffiller.com
Understanding these concepts is crucial for navigating the world of geometry. From building bridges to designing buildings, parallel and perpendicular lines are the building blocks of countless structures. In this guide, we’ll explore the fundamentals, delve into key concepts, and even provide practical examples to help you master these essential geometric relationships.
Parallel and Perpendicular Lines: The Fundamentals
Parallel lines are like two trains running on separate tracks – they never intersect. They share the same direction and slope, meaning they maintain a constant distance apart. Consider the two sides of a rectangular table – they are parallel to each other. On the other hand, perpendicular lines are like the crossbars of a ladder – they meet at a right angle (90 degrees). Think of the walls of your room – they are perpendicular to the floor.
The properties of parallel and perpendicular lines are interwoven. Imagine a line cutting through two parallel lines. The angles formed on either side of the intersecting line are equal, creating corresponding angles. This is known as the Corresponding Angles Postulate. Meanwhile, if a line is perpendicular to one of two parallel lines, it is also perpendicular to the other line. This is the Perpendicular Transversal Theorem. Understanding these postulates is key to solving a wide range of geometry problems.
Understanding Key Concepts
Slope
The slope is a measure of how steep a line is. It indicates the line’s rate of change in elevation compared to its horizontal movement. Parallel lines always share the same slope, while perpendicular lines have slopes that are negative reciprocals of each other. For example, if a line has a slope of 2, a line perpendicular to it would have a slope of -1/2.
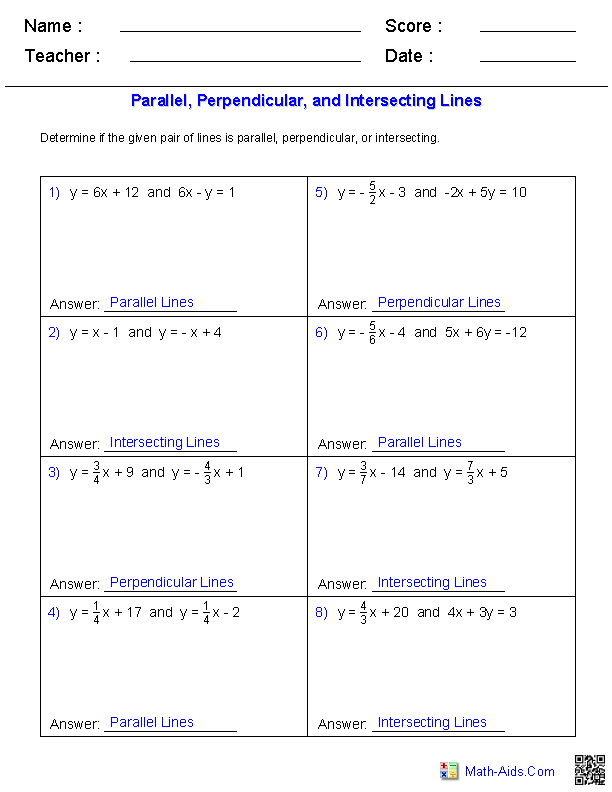
Image: learningnadeaumurther.z21.web.core.windows.net
Angle Relationships
Parallel and perpendicular lines are intimately linked with various angle relationships. These include:
- Corresponding angles: These are angles in matching positions on either side of the intersecting line, and they are equal.
- Alternate interior angles: These are angles found on opposite sides of the intersecting line and within the two parallel lines, and they are equal.
- Alternate exterior angles: Similar to alternate interior angles, but located outside the two parallel lines, these angles are also equal.
- Same-side interior angles: Located on the same side of the intersecting line and within the two parallel lines, these angles are supplementary (add up to 180 degrees).
Solving Parallel and Perpendicular Lines Problems: Practical Applications
You’ve grasped the core concepts, now let’s put them into practice. Solving problems involving parallel and perpendicular lines is not as daunting as it might seem. Here are some common problem types:
Finding the Equation of a Line
To determine the equation of a line, you need two key pieces of information: its slope and y-intercept. The slope-intercept form of a line is y = mx + b, where m is the slope and b is the y-intercept.
For example, let’s say you have a line parallel to y = 2x + 3 and passing through the point (1, 5). Since parallel lines have the same slope, the new line will also have a slope of 2. Now, you can substitute the point (1, 5) and the slope into the slope-intercept form to find the y-intercept (b). 5 = 2(1) + b, which simplifies to b = 3. Therefore, the equation of the line is y = 2x + 3.
Determining if Lines are Parallel or Perpendicular
To determine if two lines are parallel or perpendicular, you’ll again examine their slopes. If the slopes are equal, the lines are parallel. If the slopes are negative reciprocals of each other, the lines are perpendicular. For instance, the lines y = 3x + 2 and y = 3x – 5 are parallel because they both have a slope of 3. The lines y = 4x + 1 and y = -1/4x + 3 are perpendicular because their slopes are negative reciprocals of each other.
Tips and Expert Advice
Mastering parallel and perpendicular lines requires more than just memorizing formulas. It involves building a solid understanding of the underlying principles. Here’s some expert advice to help you excel:
- Visualize the concepts: Draw diagrams to represent parallel and perpendicular lines. This can help you visualize the angle relationships and understand how lines interact.
- Practice, practice, practice: Solving numerous problems is crucial to solidify your understanding of the concepts. Work through different types of problems to build confidence and improve your problem-solving skills.
- Don’t shy away from challenging problems: Push yourself beyond basic questions. Tackling complex problems will enhance your analytical abilities and deepen your comprehension of the subject matter.
- Seek help when needed: Don’t hesitate to ask for clarification from your teacher or classmates. Working together can be an effective way to resolve difficulties and strengthen your understanding.
Remember, mastering geometry is a journey, not a sprint. Be patient with yourself and celebrate your successes along the way. With persistence and a positive attitude, you can conquer Unit 3 on parallel and perpendicular lines and unlock a deeper understanding of the world around you.
FAQ
Q: What are the applications of parallel and perpendicular lines in real life?
A: Parallel and perpendicular lines are essential in numerous fields, including architecture, engineering, and construction. They are used in building structures, designing bridges, and creating blueprints for machines and furniture.
Q: How do I determine if two lines are perpendicular without knowing their slopes?
A: In a coordinate plane, if the product of the slopes of two lines is -1, then the lines are perpendicular. Alternatively, you can use the Pythagorean theorem. If the lengths of the sides of a triangle formed by the two lines and a connecting line segment satisfy the theorem, the two lines are perpendicular.
Q: What are some common mistakes to avoid when dealing with parallel and perpendicular lines?
A: One common mistake is confusing parallel and perpendicular lines. Another common error is misinterpreting slope relationships. Remember, parallel lines have the same slope, while perpendicular lines have slopes that are negative reciprocals.
Unit 3 Parallel And Perpendicular Lines Answer Key
Conclusion
Understanding parallel and perpendicular lines is essential for both academic success and life skills. By mastering the fundamentals, exploring key concepts, and applying your knowledge to solve practical problems, you can unlock a deeper understanding of geometry and its role in our world. So, are you ready to take your geometry skills to the next level?




