Have you ever looked at a map and marveled at how roads, buildings, and parks are neatly arranged? Or perhaps you’ve admired the intricate patterns in a mosaic, wondering how the artist managed to create such perfect shapes? Geometry, the branch of mathematics that deals with the study of shapes, sizes, and positions, is responsible for the order and beauty we see in our world. But before we can delve into the intricate wonders of geometry, we need to grasp its foundation: the defined terms.
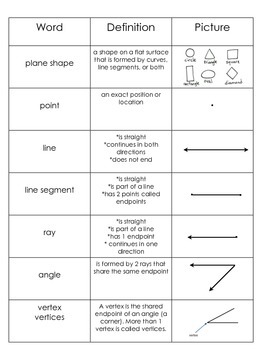
Image: www.teacherspayteachers.com
These terms are like the building blocks of a house, forming the framework upon which all geometric concepts are constructed. Understanding these terms unlocks the door to a deeper appreciation of the subject and empowers you to explore its complexities with confidence. Just like a carpenter needs to know the uses of various tools to build a beautiful structure, mastering the defined terms in geometry provides you with the essential vocabulary to navigate the world of shapes and lines.
A Journey into the World of Geometric Definitions
Let’s embark on a journey to uncover the meaning and significance of some key terms in geometry. Imagine a blank canvas – this represents our understanding of geometry. Each term we learn becomes a brushstroke, adding complexity and vibrancy to our understanding.
1. Point: The Starting Block
A point is the most basic element in geometry. It’s like a tiny dot, representing a single location in space without any dimension. We can think of a point as the tip of a pencil or the center of a circle; it has no length, width, or height. Despite its lack of size, a point is fundamental; it defines the starting point for countless geometric constructs.
2. Line: A Pathway Through Space
A line is formed by connecting two points. It extends infinitely in both directions, representing a straight path that has only length, but no width or height. Imagine a straight, perfectly flat road stretching to the horizon – that’s an example of a line. Lines are essential for defining boundaries, angles, and other geometric figures.
Image: www.math-salamanders.com
3. Plane: A Flat, Infinite Surface
A plane is a flat surface that extends infinitely in all directions. Imagine a piece of paper, but imagine it spanning infinitely without any edge. It has length and width but no thickness. Think of a tabletop or the surface of a calm lake – they portray the concept of a plane. Planes serve as the foundation for many two-dimensional geometric figures, like triangles and squares.
4. Angle: A Measure of Turn
An angle is formed by two rays, which are parts of a line that extend infinitely in one direction. The point where the rays meet is called the vertex. The angle’s measure tells us how much one ray has turned relative to the other. We measure angles in degrees, with a right angle being 90 degrees and a straight angle being 180 degrees. Angles are everywhere in our world – from the corners of buildings to the hands of a clock.
5. Segment: A Portion of a Line
A line segment is a part of a line that is bounded by two points. Imagine you have a line that extends infinitely, but you cut out a portion of that line – that’s a line segment. It has a specific beginning and end, unlike a line which continues indefinitely. We can measure the length of a line segment, which helps us determine distances and sizes in geometric figures.
6. Ray: A Semi-Infinite Line
A ray is a part of a line that starts at a specific point and extends infinitely in one direction. It’s like a line segment that continues forever. Imagine a spotlight shining across a stage; the path of the light is a ray. A ray is important in geometry as it forms an angle with another ray, creating the corner of shapes like triangles and quadrilaterals.
7. Polygon: A Closed Figure with Sides
A polygon is a closed figure formed by three or more line segments called sides. Each side intersects with exactly two other sides at their endpoints, creating vertices. Familiar polygons include triangles, squares, and pentagons. Polygons are essential for representing shapes in the real world – from the walls of a house to the slices of a pizza.
8. Circle: A Perfect Curve
A circle is a closed curve where all points on the curve are the same distance from a central point called the center. Imagine a string tied to a fixed point – if you hold the string taut and trace a path, you will create a circle. Circles appear in various aspects of our lives, from the wheels of a car to the patterns on a flower.
9. Perimeter: The Distance Around a Shape
The perimeter of a polygon is the total length of all its sides. Think of a fence surrounding a garden or a track around a field – the perimeter represents the length of the boundary. Being able to calculate perimeter is helpful in various situations, such as when finding the amount of tape you need to wrap a gift or determining the length of track you need to walk or run.
10. Area: The Space Inside a Shape
The area of a polygon is the total amount of space enclosed by its sides. Imagine painting a wall – the area of the wall represents the amount of paint you will need. Area is a crucial concept in many fields, such as calculating the space needed for a room, planning for landscaping, or determining the size of a field.
11. Volume: The Space Occupied by a Solid
Volume is used for three-dimensional figures like cubes, spheres, and pyramids. It measures the amount of space a solid takes up. Imagine filling a box with sand – the volume of the box represents the amount of sand you can fit inside. Volume is essential for calculating the capacity of containers, determining how much water a pool can hold, and understanding the size of buildings and other structures.
12. Congruence: Identical Shapes
Two figures are congruent if they have the same shape and size. They are basically identical copies of each other. Imagine two identical squares – they are congruent. Understanding congruence is useful in various real-world situations, like finding matching tiles for flooring or creating symmetrical designs.
13. Similarity: Similar Shapes with Different Sizes
Two figures are similar if they have the same shape but different sizes. Imagine two squares, one larger than the other. They are similar because their angles are the same, but their sides have different lengths. Similarity is vital in fields like architecture, where scaled models are used to represent buildings.
Expert Insights and Actionable Tips
Mastering geometric definitions is like learning a new language. It opens doors to a rich world of mathematical reasoning and problem-solving. Many renowned mathematicians and engineers emphasize the importance of understanding basic terms, stating that complex geometric concepts are much easier to grasp when you have a strong foundation in the basics.
Here are some actionable tips that can help you solidify your understanding of the defined terms:
- Visualize: Try drawing or sketching the figures. It helps you engage with the terms and see them in action.
- Connect to Real Life: Look for examples of these geometric shapes and figures in your everyday life.
- Practice: Solve practice problems and work through exercises to strengthen your understanding.
- Ask Questions: Don’t hesitate to ask your teacher, tutor, or classmate for clarification if you encounter any difficulties.
What Are The Defined Terms In Geometry
Conclusion: Unlocking the Secrets of Geometry
Stepping into the world of geometry requires understanding its fundamental vocabulary. These defined terms are not just words; they are gateways to exploring shapes, sizes, and positions in our world. By comprehending them, you gain the ability to analyze patterns, solve problems, and appreciate the elegance of geometric relationships. So, embark on your journey of discovery – the world of geometry awaits!




