Remember those days in Algebra 1 when you were first introduced to the concept of functions? You learned to identify them, graph them, and even solve for unknown values. Now, in Algebra 2, we dive deeper into the world of functions, exploring their domain and range. These terms, often seen as intimidating, act as the foundation for understanding the behavior and limitations of functions. But don’t worry, with the help of a well-crafted Algebra 2 Domain and Range worksheet and its trusty answer key, conquering this part of math can be a breeze.
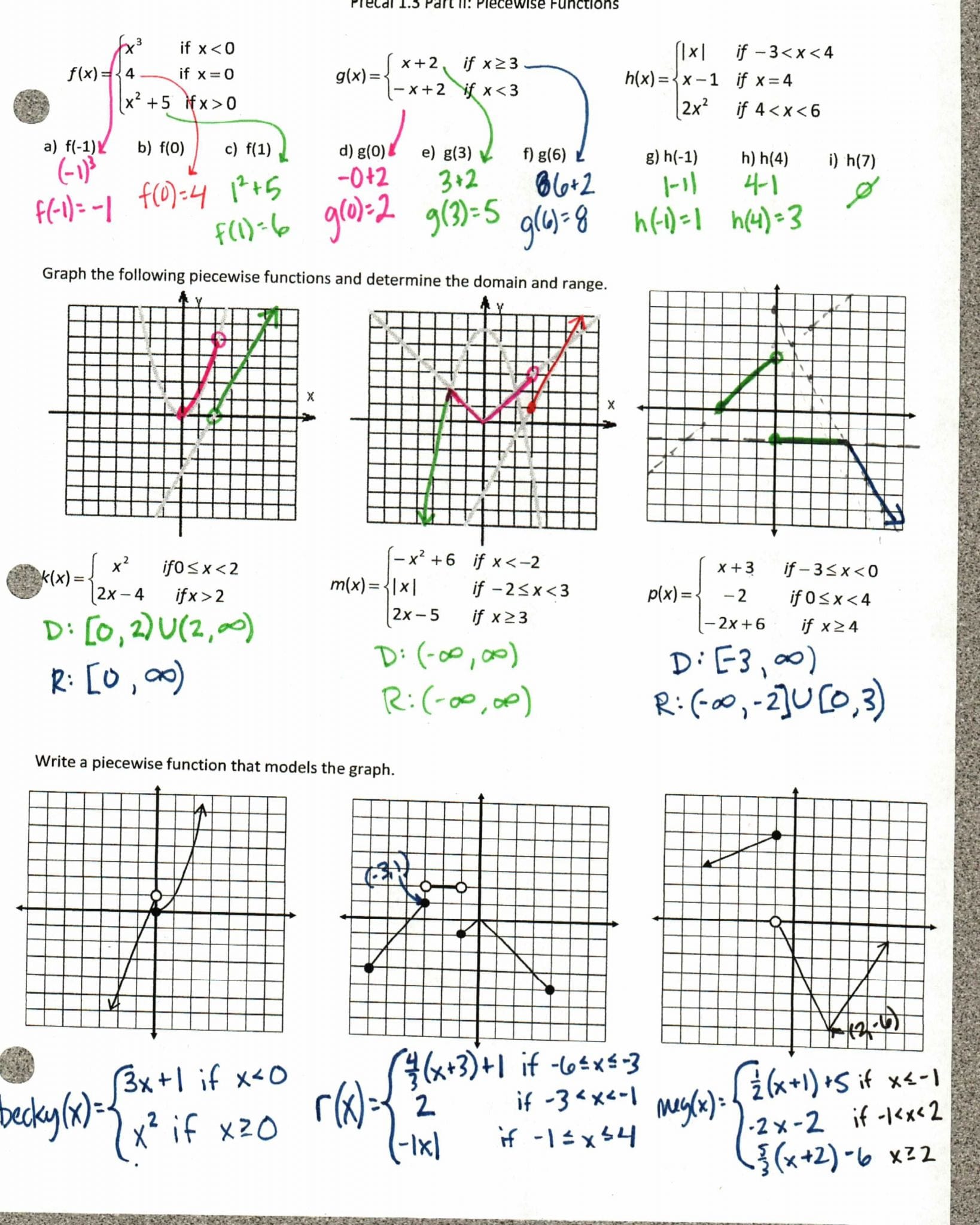
Image: db-excel.com
The beauty of these worksheets is in their ability to provide a structured environment for practice and understanding. Whether you’re struggling with a specific type of function or simply need reinforcement, these worksheets become your go-to tool, guiding you through the intricacies of domain and range. But what exactly are domain and range and what makes these concepts so important in the wider world of mathematics?
Understanding Domain and Range: The Foundation of Function Analysis
To grasp the essence of domain and range, we need to first understand what a function is. In simple terms, a function is like a machine. It takes an input, performs a predefined operation on it, and then outputs a result. The domain of a function is the set of all possible input values, the “ingredients” that the function can accept. The range, on the other hand, is the set of all possible output values, the “dishes” the function can produce.
Think of a vending machine. The domain consists of all the different button combinations. Each button combination represents an input. The range consists of all the possible snacks or drinks that the vending machine can dispense. Each item dispensed represents an output. Now, let’s dive deeper into how we can determine the domain and range of a particular function.
Identifying Domain and Range: A Step-by-Step Guide
When determining the domain and range, we need to consider the specific function. Here’s a breakdown of the process:
1. Domain:
- Identify restrictions: Look for any values that the independent variable (typically ‘x’) cannot take on. These might include fractions with zero in the denominator or square roots of negative numbers.
- Express the domain: Use interval notation, set notation, or inequalities to clearly define those acceptable values for the input ‘x’.

Image: answerlistsandra.z13.web.core.windows.net
2. Range:
- Analyze the function: Determine the lowest and highest possible output values (typically ‘y’). This might involve graphing the function or identifying its maximum and minimum values.
- Express the range: Similarly to the domain, describe the range using interval notation, set notation, or inequalities.
Examples of Domain and Range in Action:
Let’s illustrate this process with some examples.
Example 1:
f(x) = 2x + 1
In this linear function, there are no restrictions. We can input any real number, and the function will produce a corresponding output. Therefore, the domain is all real numbers, and the range is also all real numbers.
Example 2:
f(x) = √(x + 2)
Here, we have a square root function. The expression under the radical cannot be negative. Therefore, we need to ensure ‘x + 2’ is greater than or equal to zero:
x + 2 ≥ 0
x ≥ -2
The domain is all real numbers greater than or equal to -2. The range, since the square root always produces non-negative values, is all real numbers greater than or equal to 0.
Example 3:
f(x) = 1/(x-3)
This function has a restriction: the denominator cannot be zero. Therefore, we need to exclude the value of x = 3:
The domain is all real numbers except for x = 3.
The range is all real numbers except for y = 0, as the function can never output zero.
These examples demonstrate how to analyze various types of functions and determine their domain and range. As you progress in Algebra 2, you will encounter more complex functions, but the fundamental principles of domain and range will always apply.
Essential Tips for Mastering Domain and Range:
While understanding the concepts is crucial, effective practice is key to solidifying your grasp of domain and range. Here are some tips to help you excel in this area:
- Practice Regularly: Work through as many practice problems as possible. The more functions you analyze, the more comfortable you will become with the techniques.
- Visualize with Graphs: Graphing functions can provide a powerful visual representation of their domain and range. Think of the domain as the horizontal extent of the graph and the range as the vertical extent.
- Seek Help: If you encounter difficulties, don’t hesitate to seek help from your teacher, tutor, or classmates. Collaboration can be a great learning tool.
- Engage in Online Resources: Many online resources, including videos and interactive exercises, can supplement your learning. These resources offer diverse perspectives and can help you solidify your understanding.
These tips, combined with thorough practice, will set you on the path to mastering domain and range in Algebra 2. By understanding these concepts, you will develop a deeper understanding of the behavior and limitations of functions, a foundation for your continued mathematical journey.
Frequently Asked Questions about Algebra 2 Domain and Range:
1. What is the difference between domain and range?
The domain refers to the set of all possible input values a function can accept. The range, on the other hand, is the set of all possible output values the function can produce.
2. What are some common restrictions on the domain?
Common restrictions on the domain include:
- Zero in the denominator of a fraction
- Negative values under a square root
- Logarithms of non-positive numbers
3. How can a graph help determine the domain and range?
The domain represents the horizontal extent of a graph. Look for the leftmost and rightmost points on the graph to determine the domain. The range represents the vertical extent of a graph. Look for the lowest and highest points on the graph to determine the range.
4. Why is understanding domain and range important?
Understanding domain and range allows you to understand the limitations of a function. It helps determine what input values are possible and what output values are achievable. It is a fundamental concept for working with functions and applying them in real-world scenarios.
Algebra 2 Domain And Range Worksheet Answer Key
Conclusion:
Mastering domain and range in Algebra 2 is essential for understanding the behavior of functions. By practicing regularly, visualizing graphs, and seeking help when needed, you can solidify your understanding of this crucial concept. Remember, the domain and range are not just abstract ideas; they help us analyze the real applications of functions in various fields, from engineering to economics.
Are you ready to tackle the world of domain and range with confidence? What are your favorite strategies for determining domain and range? Share your thoughts and experiences below!




