Ever wondered how a function “behaves” when given different inputs? That’s where the concept of domain and range comes in, acting like a map for understanding the limits and possibilities of a function. It’s a fundamental concept in mathematics, especially when venturing into higher-level concepts like calculus. Today we’re diving into Domain and Range Worksheet #1 – uncovering the answers and unraveling the logic behind them.
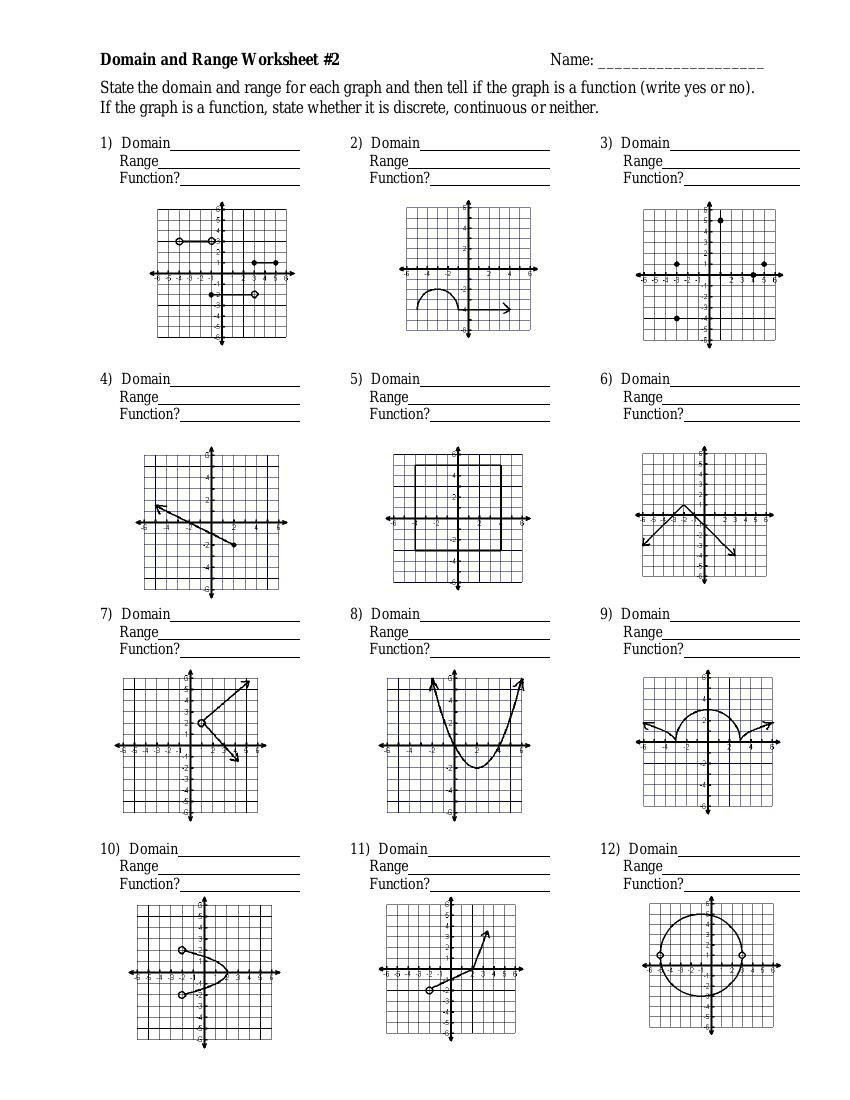
Image: worksheetlibmasten.z13.web.core.windows.net
Understanding domain and range is like understanding the blueprint of a house. The domain is the list of all possible inputs (or x-values) you can put into the function, while the range is the set of outputs (or y-values) you could possibly get back. So, you’re essentially learning how to predict the possible outcomes based on the inputs you provide.
Domain: What Goes In?
Think of the domain as the “allowed” numbers you can feed into your function. Sometimes, there are restrictions. These restrictions can arise due to several reasons:
- **Dividing by zero:** A function cannot have a zero in the denominator. For example, in the function f(x) = 1/x, x cannot be 0.
- **Square roots:** We can’t take the square root of a negative number. For example, in the function g(x) = √x, x must be greater than or equal to zero.
- **Logarithms:** The argument of a logarithm must be positive. For instance, in the function h(x) = log(x), x must be greater than 0.
Range: What Comes Out?
The range is the collection of all the “outputs” your function can produce based on the allowed inputs. It’s like the spectrum of possible values you can get.
To find the range, you often need to consider:
- **The nature of the function:** Is it linear, quadratic, or exponential? What kind of graph does it have?
- **The restrictions on the domain:** These directly influence the potential outputs.
- **Visualizing the graph:** Sometimes, a visual representation can quickly reveal the range.
Let’s Break Down Domain and Range Worksheet #1
Now, let’s take a look at some of the typical problems you might find on a Domain and Range Worksheet #1. We’ll use examples to understand the concepts in action.
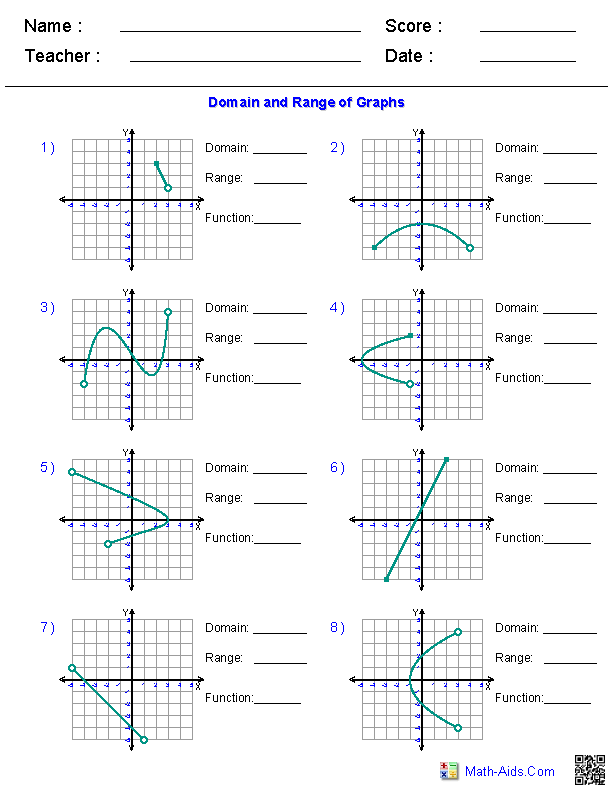
Image: omnichannelretailingforum.com
Example 1: f(x) = x + 2
Domain: All real numbers. The function is linear, so there are no restrictions.
Range: All real numbers. Since the function is linear, it will cover all possible y-values.
Example 2: g(x) = √(x-1)
Domain: x ≥ 1. We can’t take the square root of a negative number, so the expression under the radical (x-1) must be greater than or equal to zero. This gives us x – 1 ≥ 0, leading to x ≥ 1.
Range: y ≥ 0. The square root of a non-negative number is always non-negative. Therefore, the range is all real numbers greater than or equal to zero.
Example 3: h(x) = 1/(x-3)
Domain: All real numbers except x = 3. We can’t have a zero in the denominator, so x – 3 cannot be zero. This means x ≠ 3.
Range: All real numbers except y = 0. As x approaches 3, the function becomes arbitrarily large or small, never quite reaching 0.
Why are Domain and Range Important?
You might wonder, why go through all this trouble of understanding domain and range? Why are these concepts so crucial? Here’s why:
- Understanding the limitations: Domain and range help you analyze real-world situations and predict the feasible outcomes, like deciding the safe operating parameters of a machine or calculating the practical range of a projectile.
- Identifying patterns: By working with domain and range, you can recognize patterns in functions and even spot potential inconsistencies or errors.
- Building a foundation: It provides the basis for understanding more complex mathematical concepts like calculus, where you’ll be working with limits and derivatives that are heavily reliant on domain and range.
Domain and Range in Real-World Scenarios
Domain and range aren’t just abstract mathematical concepts; they have practical applications in various fields.
- Physics: Consider a model for projectile motion. The domain would be the time elapsed, while the range would represent the possible heights or distances the projectile can achieve.
- Economics: In economic models, domain can represent factors like price, and range might be the resulting quantity demanded or supplied.
- Engineering: Domain might represent the input voltage in an electronic circuit, while the range could be the resulting output current.
Domain And Range Worksheet #1 Answer
Expanding Your Knowledge
Domain and range are stepping stones to exploring the vast world of functions and their applications. Understanding these concepts opens doors to a deeper comprehension of mathematics and how it can model the world around us.
As you continue your journey in mathematics, remember that domain and range are like the compass and map that guide you through complex functions and their behavior.
Feel free to explore further resources, delve into more intricate function types, and delve deeper into the diverse applications of domain and range. The world of functions is vast and exciting, waiting to be discovered!




