Have you ever stared at a graph, wondering how a function behaves as it gets infinitely close to a certain point? Or pondered how a slight change in input can drastically alter a function’s output? These questions are at the heart of calculus, and they lead us to the fascinating world of limits and continuity. Limits are like a detective story, piecing together the behavior of functions as they approach specific points, while continuity lets us understand how smoothly functions transition from one point to the next.
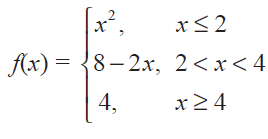
Image: www.onlinemath4all.com
This journey into limits and continuity problems will not only equip you with the tools to solve them but also reveal their significance in various scientific fields, from physics and engineering to economics and biology. Ready to embark on this exploration? Let’s begin!
The Essence of Limits: Unveiling the Behavior of Functions
Imagine you’re driving towards a destination on a winding road. As you get closer, you can see the road’s final curve, and you can almost predict where you’ll end up. This is analogous to how limits work. We examine the behavior of a function as its input gets arbitrarily close to a specific value, without actually reaching it. It’s about understanding the function’s “intended” destination.
Mathematically, we express the limit of a function f(x) as x approaches a value ‘a’ as:
lim(x->a) f(x) = L
This means that as x gets closer and closer to ‘a’, the value of f(x) gets arbitrarily close to ‘L’.
Types of Limits
There are different types of limits, each shedding light on a specific aspect of a function’s behavior:
- One-sided limits: These limits explore the function’s behavior as x approaches ‘a’ from either the left or the right side. This is like approaching a destination from different directions on a map.
- Two-sided limits: These limits consider the behavior of a function as x approaches ‘a’ from both sides. This is like approaching a destination along the entire road without having to choose a specific direction.
- Infinite limits: These limits examine what happens to a function as its input gets infinitely large or small. It’s like zooming into a graph and observing its asymptotic behavior.
Understanding Continuity: Seamless Transitions in Functions
Imagine a smooth, continuous road without any bumps or breaks. Now, imagine a road with abrupt gaps or sudden cliffs. In mathematics, this is analogous to continuity and discontinuity. A continuous function is like the smooth road – it can seamlessly transition from one point to the next without any jumps or holes. Conversely, a discontinuous function is like the broken road – it has points where it’s undefined or experiences sudden leaps.
A function is considered continuous at a point ‘a’ if it meets these three conditions:
- f(a) is defined: The function exists at the point ‘a’.
- lim(x->a) f(x) exists: The limit of the function as x approaches ‘a’ exists.
- lim(x->a) f(x) = f(a): The limit of the function as x approaches ‘a’ is equal to the value of the function at ‘a’.

Image: gbu-hamovniki.ru
Tackle Limits and Continuity Problems with Confidence
Now, let’s delve into practical examples and techniques for solving limits and continuity problems:
Example 1: Finding the Limit of a Function
Problem: Find the limit of f(x) = (x^2 – 1) / (x – 1) as x approaches 1.
Solution: We can’t simply substitute x = 1 into the function because it would result in division by zero, an undefined operation. Therefore, we need to use algebraic manipulation. We can factor the numerator:
f(x) = (x^2 – 1) / (x – 1) = (x + 1)(x – 1) / (x – 1)
Now, we can cancel out the (x – 1) terms:
f(x) = x + 1
Therefore, the limit as x approaches 1 is:
lim(x->1) f(x) = lim(x->1) (x + 1) = 1 + 1 = 2
Example 2: Determining Continuity at a Point
Problem: Determine whether the function f(x) = x^2 if x < 2, 4 if x = 2, x + 2 if x > 2 is continuous at x = 2.
Solution: Let’s check the three conditions for continuity at x = 2:
-
f(2) is defined: f(2) = 4, so the function is defined at x = 2.
-
lim(x->2) f(x) exists: We need to consider the one-sided limits:
- lim(x->2-) f(x) = lim(x->2-) x^2 = 4
- lim(x->2+) f(x) = lim(x->2+) (x + 2) = 4
Since both one-sided limits exist and are equal, the two-sided limit also exists and is equal to 4.
-
lim(x->2) f(x) = f(2): We’ve already found that lim(x->2) f(x) = 4 and f(2) = 4. Therefore, the limit and the function value are equal at x = 2.
Since all three conditions are satisfied, the function f(x) is continuous at x = 2.
Mastering Limits and Continuity: Your Path to Success
Understanding limits and continuity is essential for comprehending the fundamental building blocks of calculus and its applications. By mastering these concepts, you’ll not only be able to solve problems but also gain deeper insights into the intricate world of functions and their behaviors.
Additional Resources:
For further exploration, here are some valuable resources:
- Textbooks: “Calculus” by James Stewart, “Calculus: Early Transcendentals” by Howard Anton
- Online Courses: Khan Academy, MIT OpenCourseware
- Practice Problems: “Calculus Problems Solved” by Michael Spivak
By immersing yourself in these resources and practicing consistently, you’ll conquer limits and continuity problems with confidence. Remember, the path to mastery is paved with dedication and perseverance!
Limit And Continuity Problems With Solution Pdf
Let’s Keep Learning Together!
Do you have any specific questions or challenges you’d like to discuss about limits and continuity? Share your insights and questions in the comments below. Let’s learn together and elevate our understanding of these crucial concepts in calculus!




