Remember those frustrating times in geometry class when your teacher would casually toss around terms like “point,” “line,” and “plane” without ever defining them? It felt like we were expected to just understand these concepts instinctively. Turns out, those fundamental geometric terms are considered undefined, acting as building blocks for all other geometric definitions and theorems. It’s like trying to build a house without bricks – impossible! In this article, we’ll delve into the world of undefined terms in geometry, exploring their significance, examples, and why they’re crucial for understanding the subject.
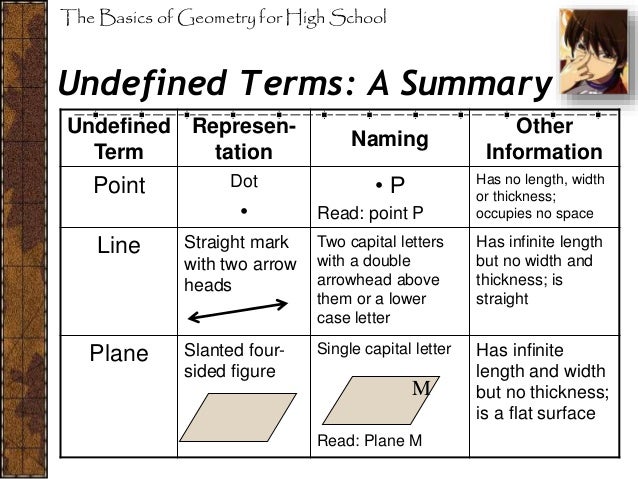
Image: www.slideshare.net
Imagine trying to explain the concept of a “triangle” to someone who has never seen one. You might try describing its three sides and three angles, but ultimately, you’d still need something concrete – a visual reference point – to truly convey the idea. This is where undefined terms come in. Just as the term “triangle” relies on the undefined concept of a “line” to be defined, all other geometric concepts rely on these fundamental building blocks.
Understanding Undefined Terms in Geometry
Defining the Undefined
In geometry, undefined terms are fundamental concepts that are not defined in terms of other geometric concepts. They are accepted as basic, intuitive ideas that form the foundation for all other geometric definitions and theorems. While they might seem like simple, self-explanatory concepts, their role is crucial for creating a consistent and logical system of geometric knowledge.
These terms are not undefined because they’re meaningless; they’re undefined because attempting to define them would lead to circular reasoning or an infinite loop of definitions. Think of it like trying to define “up” without using terms like “down” or “gravity” – it becomes a circular definition that doesn’t really explain anything. They are the building blocks of geometry, the foundation upon which all other concepts are built.
The Importance of Undefined Terms
The use of undefined terms in geometry is fundamental to the development of a logically consistent and coherent system. Instead of relying on vague or circular definitions, mathematicians choose to accept these fundamental concepts as given, creating a framework from which all other geometric ideas can be constructed.
Imagine trying to define a triangle without already understanding what a point or a line is. The definition would be incomplete and confusing. Undefined terms provide a clear starting point from which all other geometric concepts can be logically derived.

Image: study.com
Examples of Undefined Terms in Geometry
Now, let’s explore some of the most common undefined terms in geometry and how they are used to build more complex geometric concepts.
1. Point:
The simplest of all, a point is considered a location in space that has no size or dimension. It can be represented by a small dot on a piece of paper. Think of a point as being infinitely small, just a location in space.
Examples:
- The tip of a pencil
- The intersection of two lines
- A specific location on a map
2. Line:
A line is a straight path that extends infinitely in both directions. It can be defined by two points, and it has only one dimension – length.
Examples:
- The edge of a ruler
- The path of a laser beam
- The path of a plane flying straight
3. Plane:
A plane is a flat surface that extends infinitely in all directions. It can be defined by three non-collinear points (points that don’t lie on the same line).
Examples:
- The surface of a table
- The surface of a wall
- The face of a cube
4. Space:
Think of space as a three-dimensional area where all geometric figures exist. It’s the environment where our geometric figures move and interact, allowing for the exploration of shapes and dimensions beyond the flat plane.
The Evolution of Geometric Definitions
While undefined terms are considered fundamental, their understanding has evolved over time. Early mathematicians initially relied on intuitive notions, often using physical objects to represent these concepts. However, as geometry became more formalized, the need for a more rigorous foundation became evident. This led to the formalization of these terms, recognizing their role as building blocks for a consistent and logical system.
The introduction of axioms and postulates helped solidify the definitions of these fundamental terms. Axioms are statements that are assumed to be true without proof, while postulates are specific statements about geometric objects that are assumed to be true. These foundational principles then act as the starting point for deductive reasoning within geometry, allowing mathematicians to derive numerous theorems and conclusions based on these basic assumptions.
Tips and Expert Advice
Understanding the concept of undefined terms in geometry is crucial for grasping the underlying foundation of the subject. Here are some tips to help you deepen your understanding and appreciate their importance:
- Visualize: Try to visualize these undefined terms in various contexts. How would a point look like in the real world? Can you find examples of lines and planes around you?
- Relate to Definitions: Examine how these undefined terms are used to define other geometric figures. Notice how the definitions of shapes like triangles, squares, and circles all rely on concepts like points, lines, and planes.
- Think Critically: Ask yourself why these terms are considered undefined. Explore the challenges of defining them and why it’s essential to accept them as starting points.
Understanding the Logic
Think of undefined terms as the building blocks of a house. You can’t build a house without bricks, and you can’t build a comprehensive geometric system without these fundamental terms. They act as the starting point for all other definitions and theorems. Understanding their role as the foundation allows you to appreciate the logical structure of geometry.
By recognizing these basic concepts and their crucial role in defining other geometric figures, you can gain a deeper understanding and appreciation of the subject. It’s like having a map that guides you through the complexities of geometry, allowing you to navigate its diverse concepts with confidence.
Frequently Asked Questions (FAQs)
Q: Why are undefined terms necessary in geometry?
A: Undefined terms are necessary to prevent circular definitions and provide a logical foundation for the entire system. Defining these basic concepts would lead to an infinite loop of definitions.
Q: Can we define undefined terms in terms of other objects?
A: No, undefined terms cannot be defined in terms of other geometric objects. They are the fundamental building blocks, and defining them would lead to circular reasoning.
Q: Is the concept of undefined terms unique to geometry?
A: While undefined terms are prominent in geometry, similar concepts exist in other branches of mathematics, like set theory, where basic concepts like “set” and “element” are often left undefined.
Examples Of Undefined Terms In Geometry
Conclusion
As we’ve seen, understanding the concept of undefined terms in geometry is key to gaining a deeper understanding of the subject. They act as the foundational building blocks, allowing for a consistent and logical structure. By accepting these terms as starting points, we can explore the complexities of geometric shapes and figures with a clear, well-defined framework.
So, are you intrigued by the world of undefined terms in geometry? Do you feel more confident in your understanding of these fundamental concepts? Share your thoughts and questions in the comments below! Let’s further explore this fascinating aspect of geometry together.




